波特回路分析長期以來一直是電子領域的專屬工具，但是考慮到其花費和專用設備的復雜性，波特回路分析并未在工業控制領域廣泛應用。今天的高性能PLC能夠在PLC邏輯中實現波特分析，無需考慮花費和復雜度的問題。

為了維持負反饋回路的穩定性，反饋必須保持為負，這聽起來似乎毫無意義。如果在任何頻率時，回路的總相位移為360度，負反饋就會成為正反饋，回路就會變得不穩定。由于反饋回路中的減法運算本身代表的相位就是180度，所以其他回路組件的總相位不能超過180度。

圖1所示在總回路相移為360度、回路增益為2.0的時候回路是如何變得不穩定的。圖2所示包含頻率相關組件的典型控制回路的控制模塊圖。

與簡化的圖1不同，控制回路內每一個模塊的增益和相位都會隨著頻率和工作點的改變而不同。

圖2所示包含頻率相關組件的典型控制回路的控制模塊圖。我們希望控制的理想設備具有無限的帶寬（換句話說，設備在目標頻率區間內的表現是非頻率相關的）。不幸（遺憾）的是，這基本不可能。在某些頻率下，設備開始出現一些非理想化的表現有，特別是當設備包含多個不同濾波頻率的高通和低通濾波器時。這種情況下，設備建模時就要使用固定增益1.0（Gain2=1.0）和頻率為10Hz（F2=10）的低通濾波器。

    工廠濾波器之類的單組件低通濾波器在遠低于其濾波頻率（F2）時的相位移為0度，在其濾波頻率時的相移為45度，遠高于其濾波頻率時的相移為90度。類似地，在低于濾波頻率時的增益為Gain2，在濾波頻率時的增益為Gain2/√2，在高于其濾波頻率時的增益為Gain2/頻率。

    如果設備包含兩個或者多個低通濾波器，每一個濾波器都能貢獻90度的相移，總相移就可能達到180度，進而使控制回路不穩定。避免這種情況出現的常用的方法就是在回路補償模塊中引入“主導極點”。主導極點由單組件低通濾波器構成，該濾波器的頻率比設備中任何其他濾波器的頻率都要低得多。目的就是使這個濾波器（我們能夠控制）主導設備中的其他濾波器（通常我們不能控制）。

    為了達成此例中的目的，我們引入一個頻率為1Hz（F1）增益為10（Gain1）的主導極點。圖3顯示了主導極點和設備整體的相位和增益，同時顯示了總增益如何在總相位到達180度（包含減法運算時為360度）之前下降到1.0（0.0dB）以下。

圖3所示為回路組件的增益和相位，以及在單位增益下的相位。

一般來說，增益越大，控制回路將過程變量（輸出）維持在設定點（輸入）的效果就越好。但是，這之間存在一個相互制約的平衡，如果我們將回路補償的增益從10增加到20，如圖4所示，回路的相位移就會從120度增加到137度。管理這種平衡就是控制工程師的工作，他們還需要采用其他技術來提供必要的精度，同時又要維持必要的穩定性。

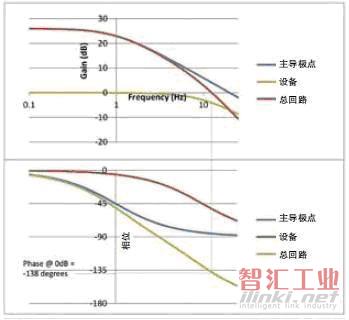
圖4所示為在更高回路增益下的增益和相位。

波特回路分析

   波特回路分析是在各種頻率下測量回路總增益和總相位移，并在系統變得不穩定之前確定裕度的一種過程。這些裕度的數值就是回路穩定性的表征。

    相位裕度就是在回路區域穩定時用360度減去回路的相位，增益裕度就是在總回路相位達到360度時的增益。相位裕度大于0（相移小于360度）的回路是穩定的，但是相位裕度越趨近于0，回路中階躍變化出現的波動就越多。根據經驗法則，45度的相位裕度通常就可以保證較好的穩定性，階躍變化的波動也不至于過多。60度的相位裕度通常可以保證非常好的穩定性，階躍變化很少或者根本沒有波動。圖3所示為控制系統相位裕度測量。

    需要注意的是在某些情況下有效的回路增益會由于組件到達自身能力極限（飽和）而開始下降。例如，觀察圖5，如果增益降低25dB，那么回路相位裕度就會降至0（0.1Hz）。如果一個階躍變化使回路中的任何一個組件達到了飽和，回路就會停滯在0.1Hz，直到波動回落到回路組件都線性運行的點上。

    基于這種原因，波特分析模塊內嵌的自動相位裕度測量功能將相位裕度定義為360度減去回路增益大于1時的最大相移。在這種定義下，圖5所示的回路相位裕度約等于5度。

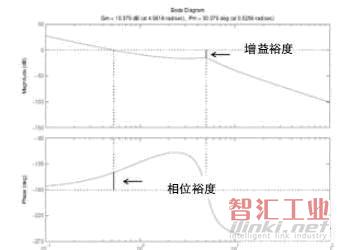
圖5所示為典型的具有增益裕度和相位裕度的波特圖（Bode plot）。